SciML Ecosystem Update: Bayesian Neural ODEs, Virtual Brownian Trees, Parallel Batching and More
Welcome to a new year! There have been a lot of exciting developments throughout the SciML ecosystem, most focusing in this case on neural and universal differential equations, expanding their functionality and providing tools for improving their performance in the hardest cases. But there's also a good set of other releases as well, such as a very high order symplectic ODE solver and a new tool for generating fast symbolic functions. Let's check it out!
Bayesian Neural ODEs in DiffEqFlux
Following our development team's latest paper on Bayesian Neural ODEs, DiffEqFlux comes equipped with new tutorials for demonstrating how to perform probabilistic estimation of neural network weights within differential equations. Thus you can check out our new tutorials and start doing automated model discovery with probabilistic estimates!
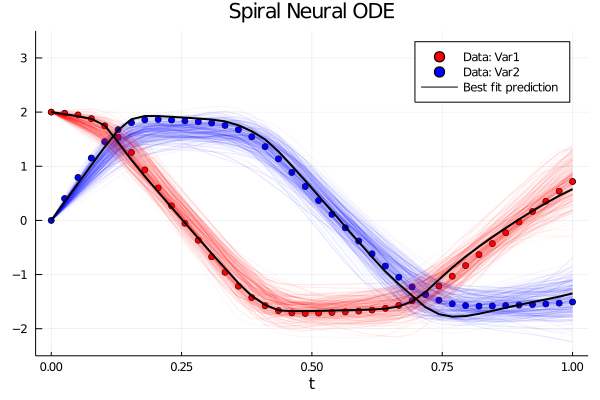
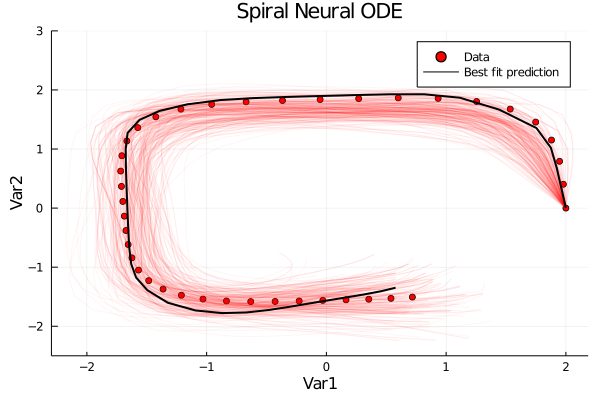
Automated Parallel Batching with EnsembleDistributed and EnsembleGPUArray with DiffEqFlux
The DifferentialEquations.jl ensemble interface is now fully compatible with the differentiation required for DiffEqFlux, meaning that all of the batching can be done on clusters and GPUs. This allows for parallelizing different solves to be done at the same time, which means minibatches can be split and computed in tandum, all in an automated fashion. For more information, check out the new tutorial. For example, the following is how to parallelize DiffEqFlux training across a cluster on a simple ODE:
using Distributed
addprocs(4)
@everywhere begin
using OrdinaryDiffEq, DiffEqSensitivity, Flux, DiffEqFlux
function f(u,p,t)
1.01u .* p
end
end
pa = [1.0]
u0 = [3.0]
θ = [u0;pa]
function model1(θ,ensemble)
prob = ODEProblem(f, [θ[1]], (0.0, 1.0), [θ[2]])
function prob_func(prob, i, repeat)
remake(prob, u0 = 0.5 .+ i/100 .* prob.u0)
end
ensemble_prob = EnsembleProblem(prob, prob_func = prob_func)
sim = solve(ensemble_prob, Tsit5(), ensemble, saveat = 0.1, trajectories = 100)
end
cb = function (θ,l) # callback function to observe training
@show l
false
end
opt = ADAM(0.1)
loss_distributed(θ) = sum(abs2,1.0.-Array(model1(θ,EnsembleDistributed())))
l1 = loss_distributed(θ)
res_distributed = DiffEqFlux.sciml_train(loss_distributed, θ, opt; cb = cb, maxiters=100)Virtual Brownian Trees: O(1) Memory SDE Solving and Adjoints
A new AbstractNoiseProcess type, the VirturalBrownianTree, has been added to the Noise Process Interface. This allows one to define a stochastic differential equation (or a random ordinary differential equation driven by an Ito process) in such a way that:
Adaptivity of the SDE solver can be used
Almost no memory is required for the noise process in the forward pass or adjoint.
To swap into this noise process, all one needs to do is use the noise keyword argument in the SDEProblem, so it's a simple switch that changes the behavior. This is useful for cases like Neural SDEs on GPUs where you may be running low on GPU memory. Big shoutout to Frank Schafer (@frankschae) for this feature!
diffeqr auto installation
diffeqr now has automated installation of Julia, meaning that R users can grab the CRAN package and do the following:
install.packages("diffeqr")
library(diffeqr)
de <- diffeqr::diffeq_setup()
lorenz <- function (u,p,t){
du1 = p[1]*(u[2]-u[1])
du2 = u[1]*(p[2]-u[3]) - u[2]
du3 = u[1]*u[2] - p[3]*u[3]
c(du1,du2,du3)
}
u0 <- c(1.0,1.0,1.0)
tspan <- c(0.0,100.0)
p <- c(10.0,28.0,8/3)
prob <- de$ODEProblem(lorenz,u0,tspan,p)
fastprob <- diffeqr::jitoptimize_ode(de,prob)
sol <- de$solve(fastprob,de$Tsit5(),saveat=0.01)and it will automatically install and use Julia in the backend. This is exciting as it's the first R package to make use of this, and I'm sure this R->Julia backend style will become more common now that it's fully automated.
New ODE Solver Package: IRKGaussLegendre.jl
We are happy to announce IRKGaussLegendre.jl as having joined the SciML family. IRKGaussLegendre.jl is an ODE solver package which implements the IRKGL16 integrator for high precision 16th order symplectic ODE solving. It's extremely efficient at what it does at the tail end of Float64 accuracy, even more efficient than the Verner methods with increasing efficiency when dropping into arbitrary precision arithmetic, and will be a nice tool in the toolbox for people looking to do high precision solving or generate reference solutions.
New Tooling Package: RuntimeGeneratedFunctions.jl
RuntimeGeneratedFunctions.jl is a very complex package for doing a simple thing: building a function at runtime with full efficiency as a normal function. This is actually quite hard because "being fast" means invoking the compiler, and invoking compilation at runtime means doing value-dependent staged computation. Thankfully, Chris Foster (@c42f) came in and saved the day, implementing a lot of key features to make this fast and world-age free. This library is now used all throughout ModelingToolkit.jl for building functions that are fully optimized and free of any world-age issues.